Calculating Standard Deviation

Standard deviation is an important measurement of dispersion within or between subgroups in a statistical sampling. Two methods for estimating standard deviation are used in quality control and quality assurance. These are the Factors Method and the Sample Standard Deviation (SSD) Method.

Estimating standard deviation using the Factors Method

The Factors Method estimates standard deviation based on the range of each subgroup, divided by a constant value (which is based on the subgroup size). This method is valid only if the total number of subgroups is greater than 10. This process variation includes only common causes.

Before you can estimate standard deviation using the Factors Method, you must calculate image\IMG00029.gif. Formulas for calculating image\IMG00030.gif are given in the previous module. Standard deviation using the Factors Method is estimated according to the following formula:

image\IMG00031.gif

image\IMG00032.gif

Subgroup size

d2

c4

2

1.128

0.798

3

1.693

0.886

4

2.059

0.921

5

2.326

0.940

6

2.534

0.952

7

2.704

0.959 

8

2.847

0.965

If the subgroup size in GainSeeker SPC is one, the range is calculated as a moving range between two consecutive values. The value for d2, therefore, is 1.128.

Estimating standard deviation using the Sample Standard Deviation Method

The Sample Standard Deviation (SSD) Method estimates standard deviation based on the distance between each point and the mean. This process variation includes both common and special causes.

image\IMG00033.gif

image\IMG00034.gif

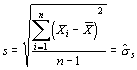
Assumptions

image\IMG00035.gif

Statistics based on the Standard Deviation Method

For Normal distributions, the following statistics use the standard deviation method chosen for capability indexes:

For other distributions, these statistics may be calculated differently. For more information, see Flow Chart Analysis of Non-Normal Data.

 

References